반응형
1. 단면 2차 모멘트(I)
- 도형에서 각각의 미소 단면적(dA)까지의 거리인 y축에 대한 거리(x), 또는 x축에 대한 거리(y)의 제곱을 곱하여 도형의 전체 면적(A)에 걸쳐 합산한 것이다.
- 재료의 외력이 가해져 굽힘 등의 변형이 발생할 때 재료의 단면적이 일정한 경우 발생하는 응력은 동일하나, 재료의 단면의 형상에 따라 굽힘의 변형 정도가 달라지므로 단면 2차 모멘트가 클수록 굽힘에 강한 재료가 된다.
- 적용 : 휨을 받는 축이나, 구조물의 휨에 대한 강성도를 구하기 위해 사용한다.
(a). x축에 대한 단면 2차 모멘트

(b). y축에 대한 단면 2차 모멘트


2. 원형 축의 단면 2차 모멘트

(a). 중실 축

(b) 중공 축

※ 여러 가지 도형의 단면 2차 모멘트



3.단면 2차 극 모멘트(Ip)
극단면 2차 모멘트, 극관성 모멘트, 단면 상승 모멘트
- 임의의 축에 대해, 미소 단면적(dA)과 좌표의 원점으로부터 미소 단면적(dA)까지의 거리(r)의 x축 관성 모멘트와 y축 관성 모멘트를 합산한 것이다.
- 즉, 미소 단면적(dA)과 좌표의 원점으로 부터 미소 단면적(dA)까지 거리의 제곱을 곱하여 총합한 것.
- 결론적으로 단면 2차 모멘트의 2배의 값을 가진다.
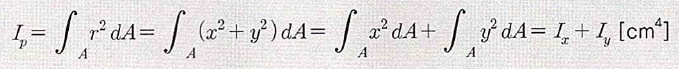
- x축과 y축이 대칭인 경우
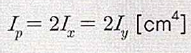
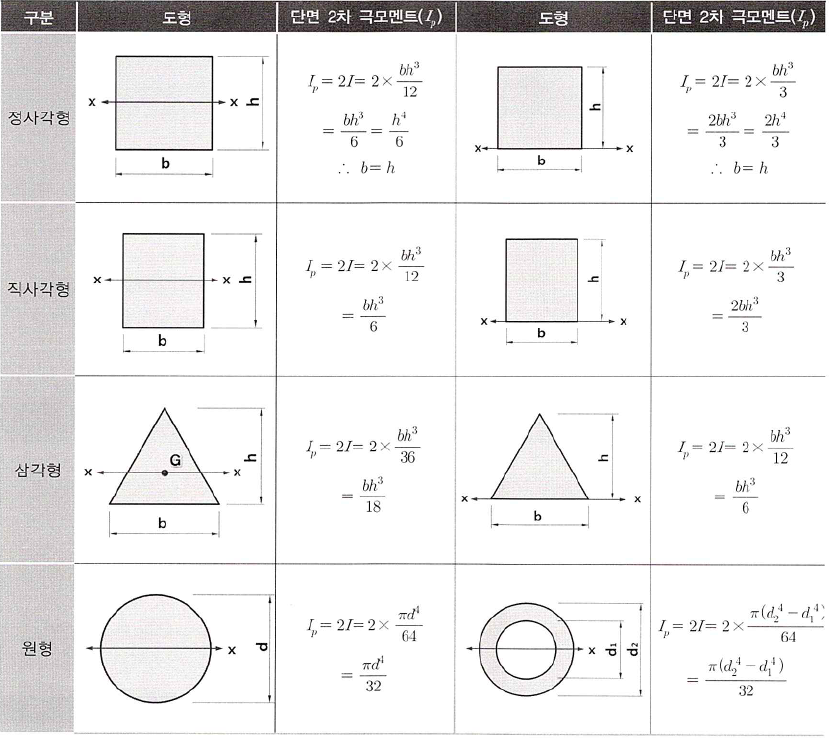
※ 여러가지 도형의 단면 2차 극모멘트(Ip)
반응형
'건설기계기술사' 카테고리의 다른 글
| 좌굴과 세장비 (0) | 2024.11.07 |
|---|---|
| 단면 계수와 회전 반경, 극 단면계수 (0) | 2024.11.07 |
| 단면 1차 모멘트와 도심 (0) | 2024.11.06 |
| 충격 응력, 카스틸리아노(Castigliano)의 정리 (0) | 2024.11.06 |
| 응력-변형률 선도(탄성한계, 항복점, 인장강도) (1) | 2024.11.06 |



