반응형
1. 충격 응력

수직으로 상단이 고정된 봉의 하단에 플랜지가 구비되고, 그 봉의 수직 축을 따라
낙하하는 추(W)를 일정위치(h)에서 낙하시켰을 때 봉은 충격방향(수직방향)으로
순간적으로 신장이 되어, 추는 봉에 대해서 최대 신장량(λ)의 형태로 일을 하게되며, 봉 내에 변형 에너지로 저장이 된다.
* 즉, 낙하하는 추의 위치 에너지는 재료 내에 탄성 에너지로 저장이 된다.
1) 추가 한 일(Wt)

2) 충격 응력(σ)

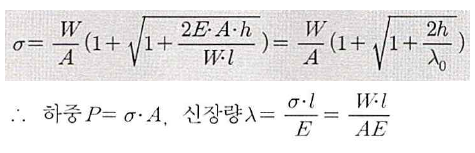
낙하높이 h=0 인 높이의 충격력만을 적용하면
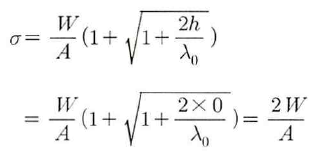
따라서, 충격 하중(급속 하중)에 의한 응력은 정하중의 2배가 된다.
3) 충격 응력에 의한 신장량 (λ)

낙하높이 h=0 인 높이의 충격력만을 적용하면

이므로, 충격하중에 의한 신장량은 정하중의 2배가 된다.
2. 카스틸리아노(Castigliano)의 정리
1) 미분 방정식을 이용한 계산

2) 면적 모멘트에 의한 계산
가). 처짐각(θ)

나). 처짐량(δ)

3) 카스틸리아노의 정리에 의한 탄성 에너지로부터의 계산
가). 작용 하중 P : 카스틸리아노의 제 1정리
탄성구조물의 변형에너지(U)를 변위(δ)의 함수로 나타낼 수 있고, 변형에너지를 변위에 대해 편미분한 값은하중(P)와같다.

나). 처짐량 δ : 카스틸리아노의 제 2정리
탄성구조물의 변형에너지(U)는 하중(P)의 함수로 나타낼 수 있고, 변형에너지를 하중에 대해 편미분한 값은변위(δ)와같다.

다). 처짐각 (θ)

라). 내부 에너지(U)
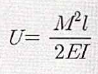
마). 적용이 불가능한 경우
- 구조물의 지점이 침하될 경우
- 온도 변화가 발생할 경우
3. 결론
- 응력 변형률곡선은 주로 재료의 비례한계 탄성한계 항복점 극한강도 신장률 등 여러 역학적 성질을 표시하는데 사용한다.
- 인장시험을 할때에는 재료의 시편을 일정한 속도로 잡아당겨 변형량을 증가시켜 그 응력을 측정하는데, 이로부터 하중변형곡선을 얻을 수 있다.
- 이 하중변형곡선으로부터 시편의 크기와는 관계가 없는 응력 변형률곡선을 구하여 인장시험의 겨로가를 나타낸다. 일반적으로 응력 변령률곡선은 공칭응력(Normal Stress)과 공칭변형률(Normal Elongation)로 나타낸다.
- 탄성변형 영역에서는 실제적인 물질의 이동이 일어나지 않기 떄문에 가해지는 힘이 풀어지면 재료는 원래 상태로 돌아간다. 그러나 항복점을 지나면 재료가 잡아당기는 힘을 견디지 못해 물질의 이동이 일어난다. 이를 소성변형 영역이라하고 가하던 힘을 풀더라도 원래 상태로 돌아가지 못한다.
- 응력변형도 곡선의 또 다른 의미는 재료에 가한 힘의 일부가 물질의 이동이라는 형태로 재료에 흡수 된다는 점이다. 즉, 가해지는 힘의 일부가 소성변형에 사용되며 여기에 사용된 힘은 탄성변형에 사용되는 힘과 달리 다시 회복되지 않는다. 따라서 연성재료의 경우에는 항복강도 이상으로 재료에 힘을 가하더라도 그 일부의 힘이 재료의 소성변형에 흡수되면서 재료가 늘어나고, 취성재료의 경우에는 소성변형이 거의 일어나지 않으므로 재료에 가해지는 힘의 모두가 그대로 파괴에 사용되어 항복강도 이상의 힘이 가해지면 순간적으로 파괴가 일어난다.
반응형
'건설기계기술사' 카테고리의 다른 글
| 단면 2차 모멘트, 단면 2차 극 모멘트 (0) | 2024.11.06 |
|---|---|
| 단면 1차 모멘트와 도심 (0) | 2024.11.06 |
| 응력-변형률 선도(탄성한계, 항복점, 인장강도) (1) | 2024.11.06 |
| 피로 강도, 피로 한도, 피로 한도 영향 인자 (0) | 2024.11.05 |
| 유압 제어 밸브의 종류와 특성 (0) | 2024.11.05 |



